Antecedentes.
El objetivo de esta contribución es presentar los argumentos
que demuestran la consecuencia de la improvisación que lleva a tomar medidas
equivocadas por parte de los gobernantes.
El 15 de junio de 2020 la pandemia tendía a la baja en la
ciudad de Hermosillo. Sin embargo,
- Entre el 16 de junio y el 15 de julio fue revertida la tendencia a la disminución de la velocidad del contagio.
- Se retrasó más de un mes el control de la pandemia.
- Se provocó una cantidad de enfermos y defunciones muy superior a las que habrían ocurrido y se impactó negativamente sobre la ya lastimada economía.
- Una cantidad no determinada, pero muy numerosa, de pequeños comercios se vieron obligados a cerrar.
La ciudad de Hermosillo, Sonora, vive una etapa especialmente
difícil en la pandemia que ha resultado de la irrupción en el mundo del virus
SARS-COV-2, causante de la enfermedad conocida como COVID-19.
El sábado 13 de junio de 2020, el Cabildo de Hermosillo y la
Presidenta Municipal, acordaron que a partir del 16 de junio siguiente se
prohibía transitar en automóvil desde las 18 horas hasta las 6 de la mañana del
día siguiente. Como se puede consultar en la prensa , éste era un capricho de
la alcaldesa, quien lo había querido imponer desde el 2 de abril anterior. No
había sustento técnico ni científico que respaldara la medida tomada.
Se restringieron los horarios comerciales y se planteó la
posibilidad de solicitar salvo conductos para tener derecho a moverse en
automóvil en ese periodo prohibido.
Ni a la presidencia municipal ni al cabildo les importó
violar la Constitución de la República, que en su Artículo 11 prohíbe la
exigencia de salvoconductos para circular por el país. Tampoco se detuvieron a
pensar que estaban usurpando las facultades del Presidente de México, pues el
Artículo 29 de la misma Constitución establece que solamente la presidencia
puede tomar esa clase de decisiones siempre y cuando así se lo apruebe el
Congreso de la Unión, o la Comisión Permanente si éste no está reunido.
La medida fue ligeramente suavizada un mes después,
ampliando el horario de circulación hasta las 9 de la noche. Sin embargo, el
daño ya estaba hecho.
Desde el domingo 14 de junio siguiente hice saber en redes
sociales que la medida anunciada operaría en contra del propósito que estaban
manifestando.
Afirmé que sería contraproducente y ahora demostraré que así
ocurrió. En otra contribución explicaré los argumentos técnicos que establecen
por qué era de esperarse que las cosas resultaran mal.
 |
| Los amaneceres y atardeceres son muy bellos en Hermosillo, pero muchas decenas de hospitalizados no lo pueden ver. |
Los
efectos de la medida.
La forma más simple de evaluar la medida aplicada en el
municipio de Hermosillo es comparar el número de casos activos por cada cien
mil habitantes en los municipios de: Hermosillo, Cajeme, Nogales y Navojoa.
Para ese propósito tomé los datos del portal del Sistema de
Información Estadística del Estado de Sonora. Su dirección es: http : // www.estadisticasonora.gob.mx/
Hasta el 18 de julio de 2020, en ésta se encuentran datos de
población de municipios desde 2014 hasta 2018. Con ellos es posible estudiar la
tasa de crecimiento promedio de un año a otro, calcular su promedio sobre esos
cinco años y proyectar la población esperada hasta el año 2020.
Con estos datos capturé los datos de casos de contagios
nuevos por semana, como se podían consultar hasta el 18 de julio de 2020 en el
siguiente portal: https://covid19data.unison.mx/
De esta manera se recurre a un sistema de medida en el que
no influye la diferencia en poblaciones de un municipio a otro y se considera
solamente su densidad.
El resultado se muestra en la siguiente gráfica:
 |
| Hermosillo fue el único municipio con ascenso vertiginoso en los días de toque de queda de 12 horas. |
En la horizontal se cuentan las semanas como las reporta el
portal de datos citado. En la vertical se consideran los casos nuevos por
semana y por cada cien mil habitantes.
El peor resultado es el del municipio de Hermosillo. Son las
líneas rojas con puntos rojos, que habían empezado a bajar después de la semana
25 a la 26 para dispararse inmediatamente desde allí hasta la semana 29. Lo
único diferente entre los municipios era la medida del toque de queda, cuando
el índice que estoy exponiendo pasó de 49.93 a 129.43 por cada cien mil
habitantes. Es decir, se multiplicó por 2.6 en treinta días mientras el resto
de municipios de Sonora tendían a la baja.
Los tres municipios mencionados en la gráfica anterior son
los más numerosos en número de casos, pero si se agrega además Navojoa, se
refuerza la afirmación anterior.
 |
| Si se incluye Navojoa se agrega otro municipio con la pandemia en descenso. El único que crece es Hermosillo. |
De nuevo se cuentan
en la horizontal las semanas como las reporta el portal de datos citado y en la
vertical se consideran los casos nuevos por semana y por cada cien mil
habitantes.
La gráfica en líneas negras con puntos rojos corresponde al
municipio de Navojoa. Crece hasta la semana 27 y disminuye después siguiendo
una tendencia similar a la de Nogales y Cajeme.
Enseguida consideramos otros dos parámetros que respaldan la
misma conclusión.
¿Por qué
usar los porcentajes de crecimiento de contagios?
El cálculo del porcentaje de incremento diario del número de
personas contagiadas de covid-19 es un parámetro importante que tiene
fundamento en las matemáticas. Quienes recuerden el trabajo de Thomas Malthus
tendrán presente que el crecimiento demográfico tiende a seguir una progresión
geométrica cuando no se encuentra con obstáculos que se le enfrente.
La misma teoría de Malthus empezó a ser modificada muy
pronto al considerar los distintos factores que pudrían afectar el número de
individuos de una especie. La rama científica se llama en ocasiones dinámica de
poblaciones.
Regresando a la teoría de Malthus, ésta establece que los
crecimientos poblacionales siguen una progresión geométrica. Por esa razón el
manejo del porcentaje es importante para detectar qué está pasando en tiempo
real.
Un ejemplo de una progresión geométrica es la siguiente: si
una población tiene A individuos y ésta crece con un porcentaje k constante cada
día, cuando transcurran tres días el número B de individuos será
 |
| Esta es una progresión geométrica. Fundamental en el análisis de epidemias y básico para definir la función exponencial. |
Pongamos un ejemplo numérico enseguida. Si A vale 1200
individuos el día lunes de cualquier fecha, y crece con porcentaje de 5%
diario, el valor de B será de 1389 en números redondos.
En cambio si el crecimiento va cambiando, y el primer día el
porcentaje es k1, después k2 y por último k3,
lo que tenemos es una expresión algebraica como la que sigue:
 |
| Constante de crecimiento variable. Si la velocidad de contagio disminuye las k-s decrecen. Si aumentan le pasa lo mismo a la velocidad del contagio. |
Pondremos ahora un par de ejemplos, uno cuando el valor de k
crece para ser 5% el primer día, 5.5% el segundo y 6% el tercer día. Si A es igual
a 1200 individuos, como antes, el valor de B será 1409.
En cambio, si los
valores son 5% el primer día, y después 4.5% y 4% respectivamente. El valor de
B será 1369.
Esas diferencias crecen si el número de días se acumula.
La
velocidad de crecimiento de los contagios.
Los
resultados con base en el porcentaje de incrementos diarios.
Calculando el porcentaje diario se encuentran gráficas muy
aleatorias. Un ejemplo es la siguiente, que presenta en la horizontal los
cocientes en los últimos 98 días. En la vertical están los porcentajes de
incremento de un día a otro y en un cuadro a la derecha los últimos 7 días. En
números negros se lee que el promedio de porcentajes de aumento de esa semana
marcada es de 4.33%. Algo preocupante como veremos después.
 |
| Los datos crudos necesitan herramientas teóricas para estudiarlos y extraer información útil. |
Esta gráfica demuestra la magnitud del problema que se desea
entender. El porcentaje fluctúa porque de manera natural es un fenómeno
aleatorio, pero también se agrega la tendencia a dejar para después el proceso
de captura de los datos. Donde los resultados de las pruebas que se realizan no
se reportan a tiempo.
Entonces se necesita agregar elementos nuevos que nos
permitan entender. Por eso he recurrido a presentar promedios cada siete días.
O bien, cada catorce días como en la gráfica siguiente:
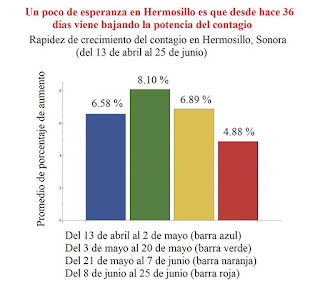 |
| En junio de 2020 el promedio de porcentajes de aumento disminuía. Aquí se presentan por catorcenas. |
Se muestra la forma en que todavía se apreciaba una
tendencia de seis semanas a la disminución de la velocidad de crecimiento de
los contagios.
Esta tendencia se ve modificada a los pocos días de que en
el municipio de Hermosillo se impone el toque de queda. Son once barras que
condensan resultados desde abril. Se aprecia el crecimiento en mayo,
seguramente como consecuencia de la insistencia de la gente en realizar sus
festejos. Después de la barra más alta se encuentran cinco barras decrecientes.
 |
| La tendencia a la disminución de la velocidad del contagio fue revertida. Empezó a crecer en los 30 días de toque de queda de 12 horas. |
¡Y entonces aparece el acuerdo para el toque de queda!
En los promedios se nota cómo la tendencia a la baja se
mantuvo hasta los últimos días de junio.
El problema se presenta en las barras IV y V, porque los
promedios de crecimiento semanales empiezan a crecer.
Veremos que otros parámetros muestran la magnitud del
impacto negativo de la medida instrumentada en el municipio de Hermosillo.
La
velocidad de crecimiento de los contagios diarios.
Los
resultados con base en el logaritmo de los datos crudos.
Un método más técnico, pero también útil, es el logaritmo de
los datos. Esto lo presentamos después de una explicación sobre qué es el
logaritmo.
En la siguiente figura listamos el número 10 elevado a
varias potencias. Escribimos también el resultado.
 |
| El logaritmo crece con lentitud mientras el resultado crece velozmente. Por eso es útil para estudiar curvas de crecimiento vertiginoso. |
Se aprecia que el resultado crece rápidamente desde 10 hasta
1000. En cambio, el exponente apenas pasa de 1 a 3. Éste último es el logaritmo
base 10. Lo importante es que el logaritmo crece muy lento.
Puede haber logaritmos base 7, o cualquier otro número.
Nosotros usaremos el logaritmo basado en el número de Euler. Denotado como e. Se le llama logaritmo
natural.
Consideremos los datos de contagios diarios en Hermosillo
como han sido reportados por las autoridades de salud del Estado de Sonora. En
la horizontal se cuentan 98 días hasta el 20 de julio. En la vertical el número
de casos de contagio que sí fueron registrados en los hospitales de Hermosillo.
 |
| Se presentan 98 días de contagios acumulados en Hermosillo. |
A estos datos le aplicamos el logaritmo que ya mencionamos y
al graficarlos se obtiene la siguiente gráfica. En la horizontal están los 98
días hasta el 20 de julio de 2020 y en la vertical el logaritmo natural de los
números de contagios diarios. Puede verse que la curva es de crecimiento más
suave. Si el crecimiento llegara a 0, la curva sería horizontal e indicaría que
ya no hay contagios. Por eso nuestro deseo es que esta curva alcance la
horizontal.
 |
| Los datos acumulados de contagios cuando se les aplica el logaritmo natural. El escenario deseado es que la curva sea horizontal. |
¿Qué tan lejos está esa curva de la horizontal?
La respuesta se puede encontrar si trazamos rectas tangentes
a esa curva y medimos su pendiente. La gráfica siguiente coincide con la
anterior pero con algunas rectas trazadas para mostrar las rectas mencionadas.
Las hemos distinguido con colores para presentar con mayor claridad que las
orientaciones cambian conforme transcurren los días:
 |
| La curva se acercaba a la horizontal, pero durante el toque de queda empezó a crecer la inclinación de nueva cuenta. |
El siguiente procedimiento consistió en segmentar los datos
en grupos de 7 días para ajustar rectas semana por semana. El ajuste
proporciona la ecuación de la recta, a partir de la cual se puede obtener la
inclinación de la recta. La gráfica que resulta es la siguiente
 |
| Las pendientes de las rectas tangentes a la curva decrecían, pero después del 16 de junio la inclinación empezó a crecer. |
En la gráfica se encuentran 11 barras. Cada una corresponde
a la pendiente de la recta ajustada para una semana específica. La más alta se
ubica en mayo. Es cuando el número de contagios crece más rápido. A partir de
allí empieza a bajar, indicando que el número de contagios crece cada vez más
lento. Con una flecha roja se marca el día en que se empieza a aplicar en
Hermosillo la medida del toque de queda. Después de ésta vienen dos barras: en
una sube ligeramente, en otra disminuye y entrando a julio vuelve a crecer.
Conclusiones:
En el análisis de casos de contagio de las 4 semanas de
aplicación de la medida de toque de queda en Hermosillo se encuentra los
siguiente:
- El número de nuevos casos de contagio semanales, por cada cien mil habitantes, creció en Hermosillo para multiplicarse por 2.6 mientras Cajeme, Nogales y Navojoa bajaban.
- El porcentaje de crecimiento diario del número de contagios, promediado por semana, aumentó del 16 de junio al 15 de julio de 2020.
- El logaritmo natural de los datos de contagio venían a la baja hasta los últimos días de junio, pero empezaron a crecer después de la segunda semana de aplicación del toque de queda en Hermosillo.
- El descenso de la pandemia fue revertido.
- El número de enfermos y de personas fallecidas aumentó.
- La apertura económica fue aplazada cuando menos un mes más.


